STABILITY IN HYDROSTATIC PHASE
When the travel speed is low, stability is mainly determined by the position of the center of hydrostatic forces (center of flotation) and the position of weight application. The displacement of a ship is a term designating the volume of water that a given weight displaces: Displacement (Liters) = weight (Kg) / Water density (Kg/m3)
Example: With a density of sea water at 20 degrees of 1023kg/m3, a board of 4.56 kg and its surfer of 31kg total a weight of 35.56kg, and displace a volume of water of (35.56)/1023 =0.03476 m3=34.76 liters. If the board has a volume greater than 34.76 liters the board floats, if the volume of the board is less than 34.76 liters the board sinks, until the surfer is submerged in the missing volume. We can determine the stability of the board, like that of a ship, by comparing the position of the submerged center of volume (displacement) and the position of application of the weight.
Let's take for example, a 75 liter wing foil board (white dots mesh), with a displacement of 34.76 liters (yellow mesh):
our example in front view :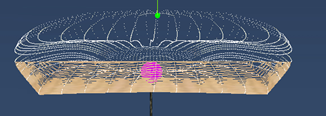 
And in side view with the tail on the left and the nose on the right :
the pink dot shows the location of the center of flotation.
himself in front of the center of flotation the board tilts forward (pitch on pitch angle), if he places himself on the side, the board tilts on the side (roll on roll angle).
The board is shown here in a state of horizontal balance, this balance is only possible if the weight is directly above the center of flotation. The position of the center of flotation at the various roll angles shows the position that the support point must occupy to ensure balance at a given roll angle and pitch. For obvious reasons of resistance to advancement, which is minimal when the frontal surface is minimal, the shaper provides, for a board in hydrostatic phase, the position of the surfer which preserves the horizontality of the pitch axis.
In the example above, the hydrostatic lift point is located 713 mm from the tail. The shaper will ensure that the longitudinal position of the center of flotation is close to that of the planing center (see planing maneuverability chapter) and foiling (see foil chapter).
This longitudinal position preserving the horizontal pitch axis in the hydrostatic phase having been acquired, the study of lateral stability (roll angle) can be carried out. Stability in roll is the most sensitive, due to the elongated shape of the boards, it is therefore the one which is determining to quantify the stability of the board.
But before moving on to the analysis of roll stability, let's take a moment to describe the method of calculating the center of flotation:
Calculation of the surfboard/foil/sup center of flotation:
Calculating the submerged volume and its center can be complex because the board shapes are curved. This calculation can be done by cutting the board into n cross sections (n = number of sections), of which the surface and center are calculated:
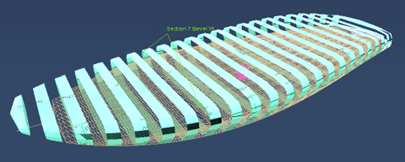
The volume of the n slices is calculated according to the surface area of the section and the distance between 2 sections. The overall volume results from the addition of the n volumes of the slices. The global center of buoyancy is a weighted average of the x,y,z coordinates of the n center points of the n sections. The “weighting” is a factor applied to the coordinates of the points, Factor=slice volume/total volume.
To determine the immersed volume for a given displacement, successive iterations of the aforementioned calculation are carried out with truncated sections, following a plane inclined at the roll angle considered. If the volume found is greater than the volume displaced, we move the cutting plane and start again until we find the correct cutting height corresponding to the volume of the displacement sought.
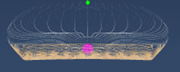iterations of submerged volume tests at roll angle 0
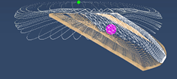
test iterations at 30° roll angle
For a given weight, therefore a given displacement, the position of this center of flotation depends on the submerged volume, which varies according to the roll angle. Each time the surfer's weight or board shape changes, these calculations must be repeated. Software will therefore be very useful for testing the various configurations, the calculation of the centers of flotation is integrated into the software.l ShaperWaveDynamics .
Surfboard/foil/wing/sup stability diagram: The curve of the lever arms.
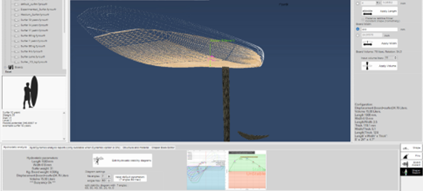
SWD software, has a hydrostatic curve editing tool. The curves presented as an example below are taken from this software
Let's keep the example of our little 31 kg surfer on a 75L board seen above, and let's edit opposite, a cross section of our board, at the distance 713 mm from the tail which maintains the horizontal pitch balance at 0 °. A calculation of the submerged volumes ensuring flotation (34.76L), at angles of 0°, 35° and 70° of roll was carried out, the points named G are the points of application of the weight (centers of the deck), the points named B are the centers of flotation. The green points and cutting profiles represent the 0° roll, the pink points the 35° roll and the gold points the 70° roll.
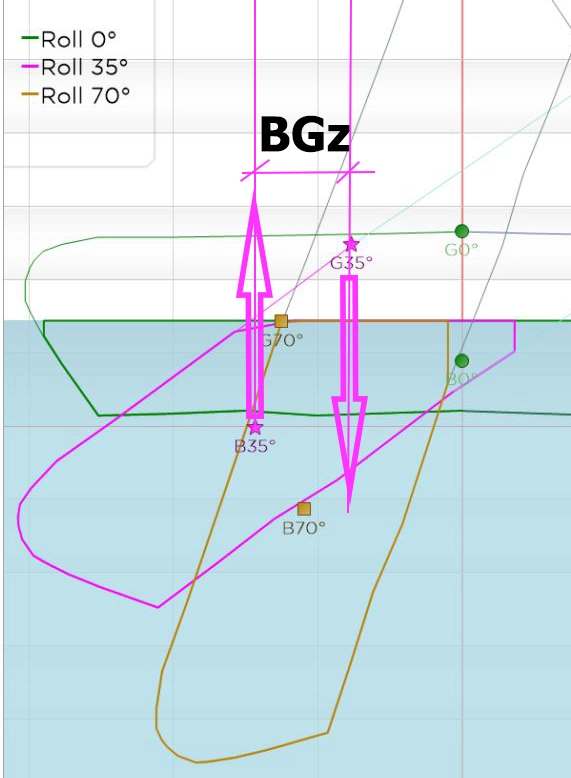
At 0° roll: the (green) points G and B are plumb, the buoyancy forces and the weight forces are aligned and opposite. The distance between the vertical lines passing through G and B is zero, this implies zero righting torque, the surfer does not feel any resistance or tilting force, he can swing the board sideways without effort and generate roll by supporting your heels or toes.
At roll 35°: (pink dots) When the board tilts at roll 35°, the submerged volume moves, the distance “BGz” between G35° and B35° is no longer zero, the buoyancy force directed towards the top, and the weight force, directed downwards, produce a positive righting torque, which opposes the increase in roll, and brings the board back to horizontal. The surfer feels a force under the toe or heel which prevents him from tilting the board. The board is stable. To maintain the board at a rolling angle of 35°, the surfer placed in the center of the bridge must exert a rolling torque of: Vertical distance between G and B (in meters) * force weight (in newtons), or else move at plumb with the center of flotation.
At roll 70°: If the surfer remains in the center of the bridge, when the board reaches 70° of roll, the center B70° passes to the other side of the point G70° and generates a distance, a lever arm, and therefore a negative torque, which tilts the board: The board becomes unstable.
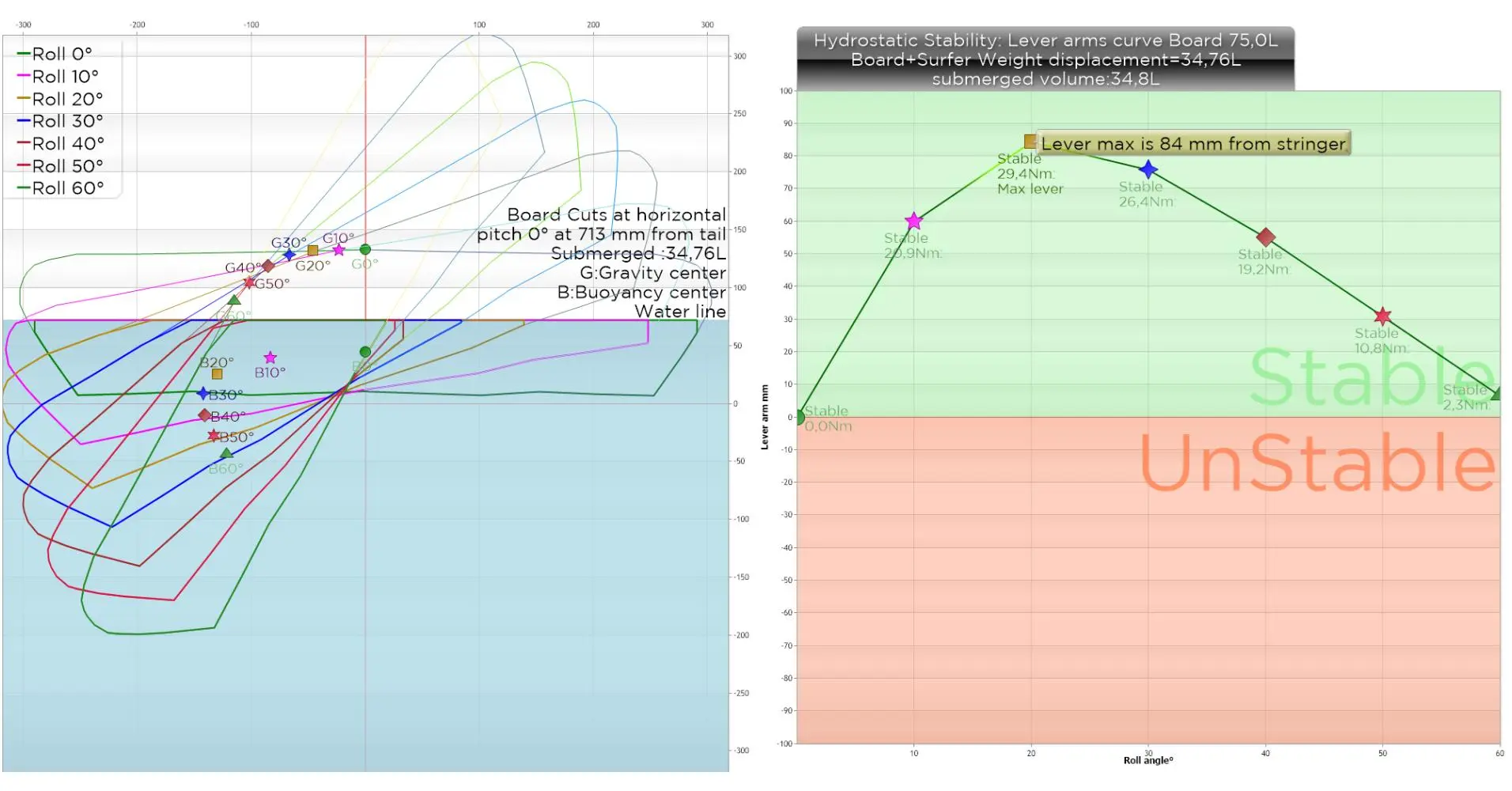
By editing lever arm curves at various roll angles, for a given surfer weight, we can precisely quantify the stability of a board.
We see below, on the left, the variation in the positions of the centers of flotation, and the corresponding curve of the lever arms, on the right. For a 31 kg surfer The maximum lever arm is 84 mm with a righting torque of 29.4Nm
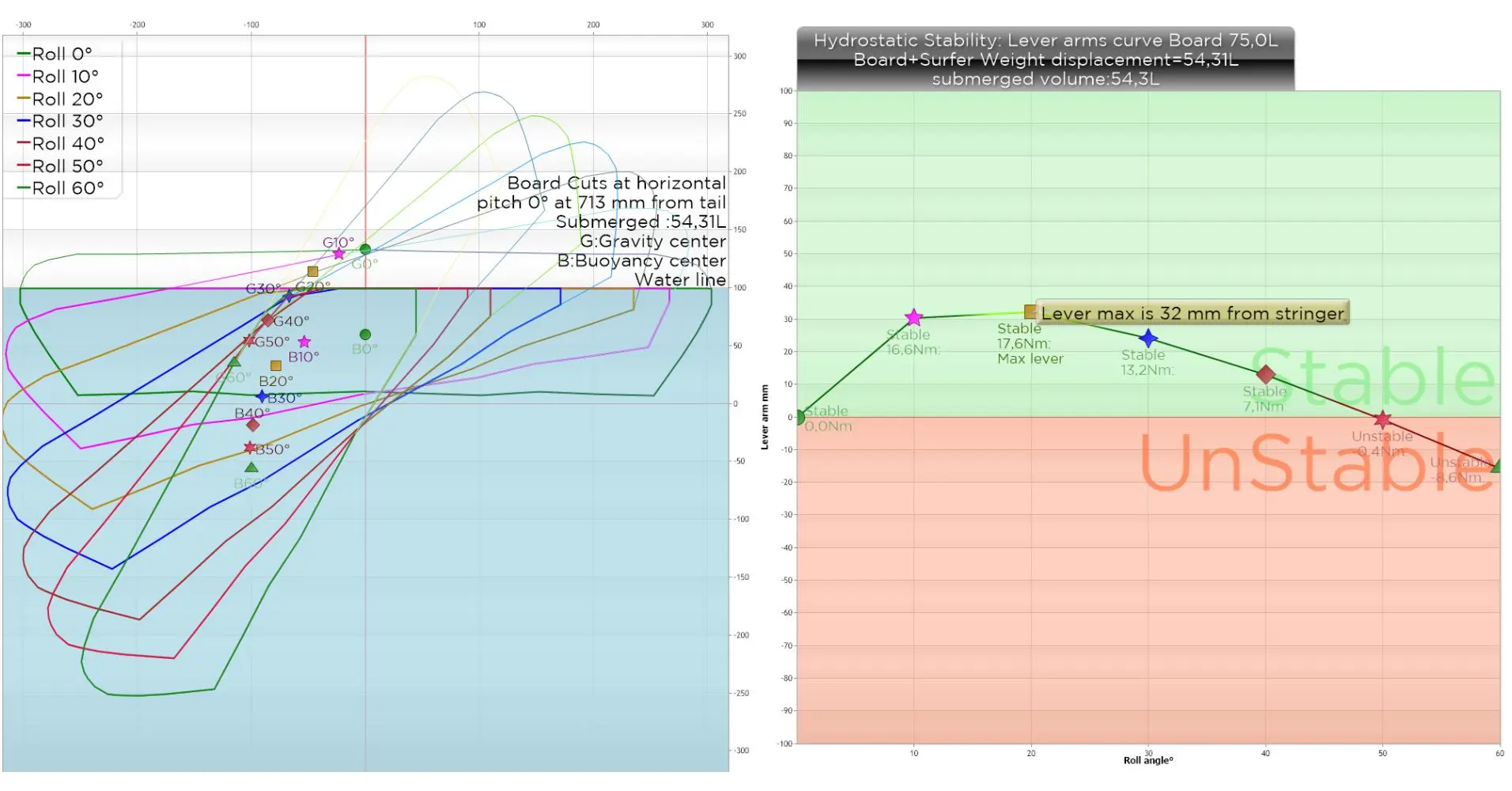
Below the same board with a 51 kg surfer. The maximum lever arm is 32 mm with a righting torque of 17.6Nm:
Below, with the same board and a 70kg surfer:
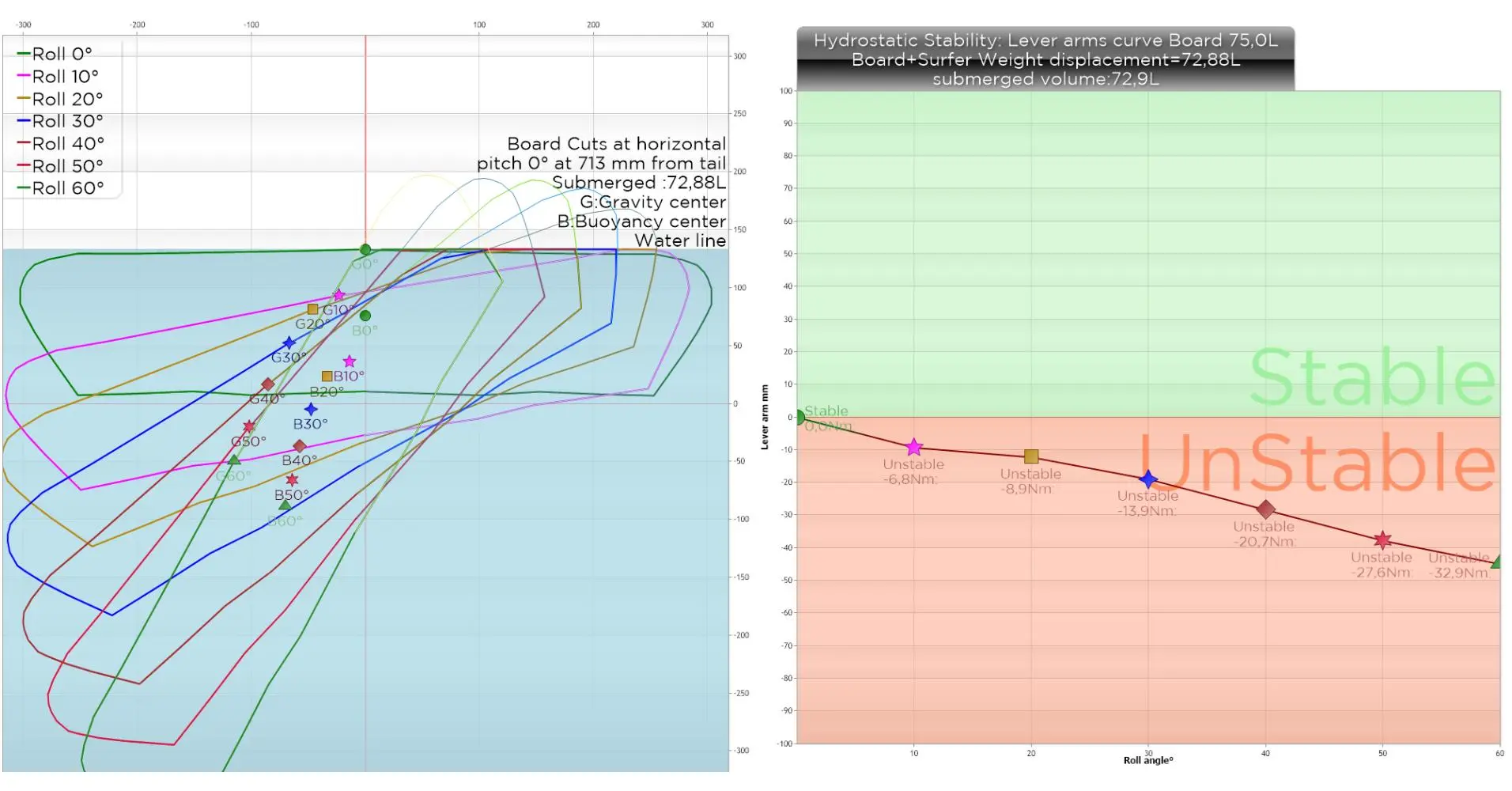
The lever arm immediately goes to negative values, the board is unstable. This is not necessarily a problem for a good level surfer not looking for stability at low speed, because he will reach the speed of planing or foiling, by controlling the attitude of the board in the hydrostatic phase by controlling the heel-toe supports, or with “foot straps” But this instability at low speed should be avoided for a surfer's board planning to stand up on the board before having reached planing speed. It is obvious that stability decreases with the board volume/displacement ratio (surfer weight). To have a minimum of stability, you must provide at least 10 liters of board volume in addition to the displacement...
Let's take our last example of a 70 kg surfer and increase the board to 80 liters while maintaining its width of 610mm, and focus our analysis on 5 roll values from 0 to 30 degrees of roll:
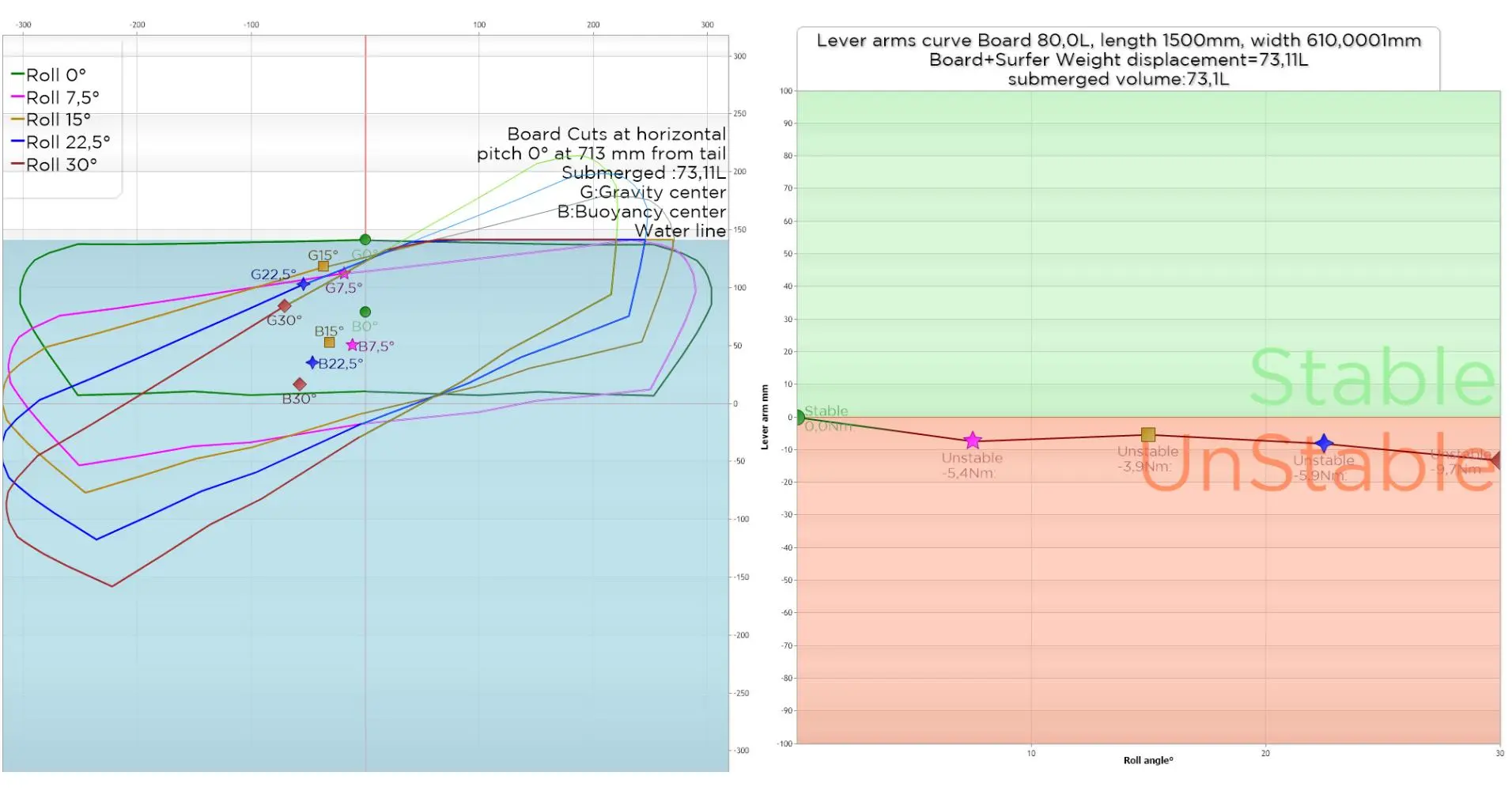
The lever arms curve (above right) is less steep, but remains in the negative zone. We will try to correct this instability by widening the board a little, going to 700 mm while maintaining the same volume:
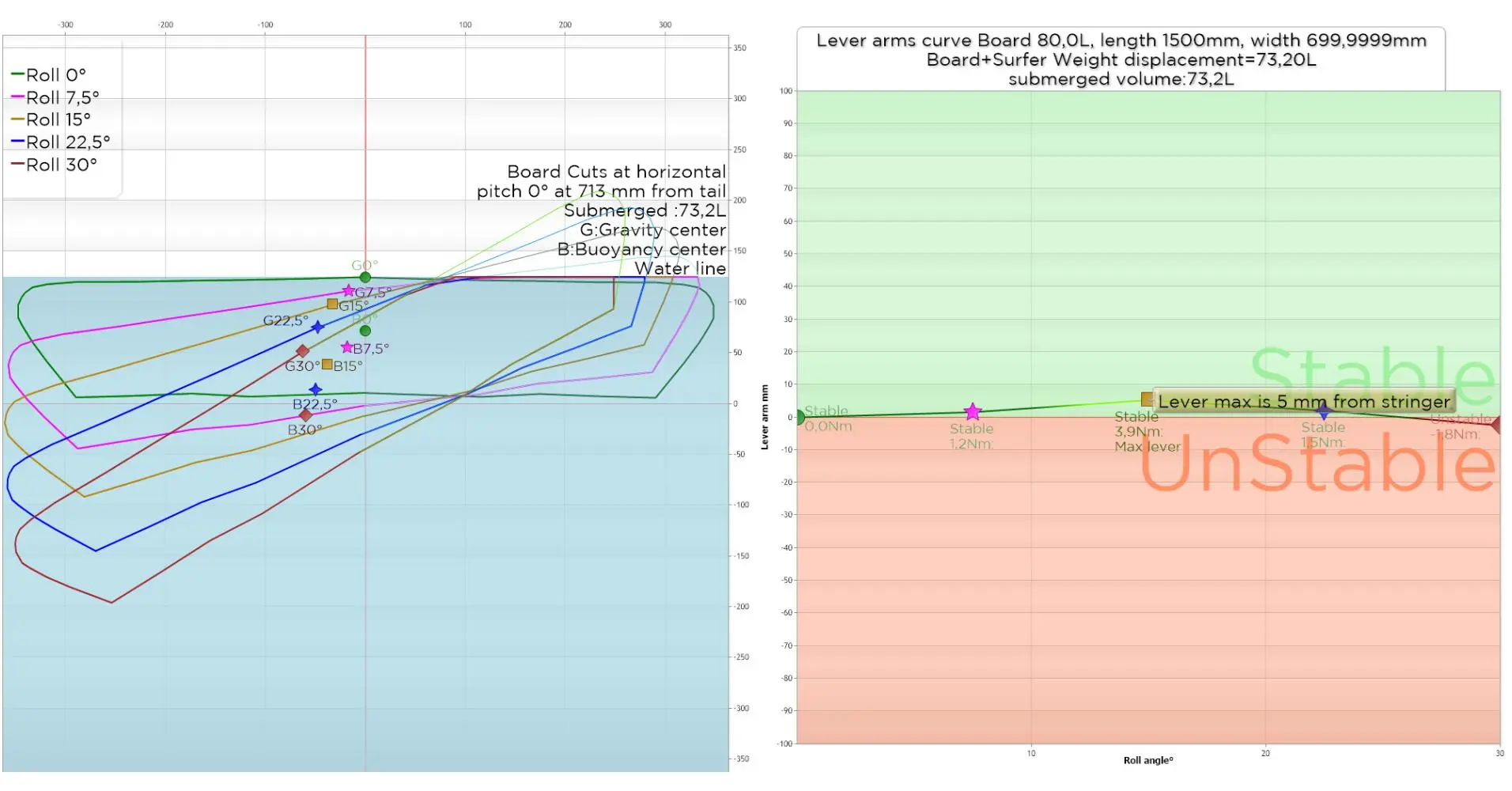
The 700 mm width provides stability (max lever arm 5mm and positive righting torque) up to 22.5° of roll.
The shaper's expertise consists of assigning stability lever arm values when designing his board, depending on the weight and level of the surfer and feedback on sensations for tested lever arm values.
Quantifying stability with lever curve allows shapers and surfers to establish knowledge bases and objective data that provide reliable insight and prediction of a board's behavior for a given surfer weight.
Note: the notion of stability described here is purely hydrostatic. A surfer with a board with a volume greater than the displacement (floating), in a rough sea of surface chop, will be able to feel greater instability, than with a board of lower volume, less than the displacement, therefore totally submerged, because it will be less subject to surface chop, in the hydrostatic start-up phase...