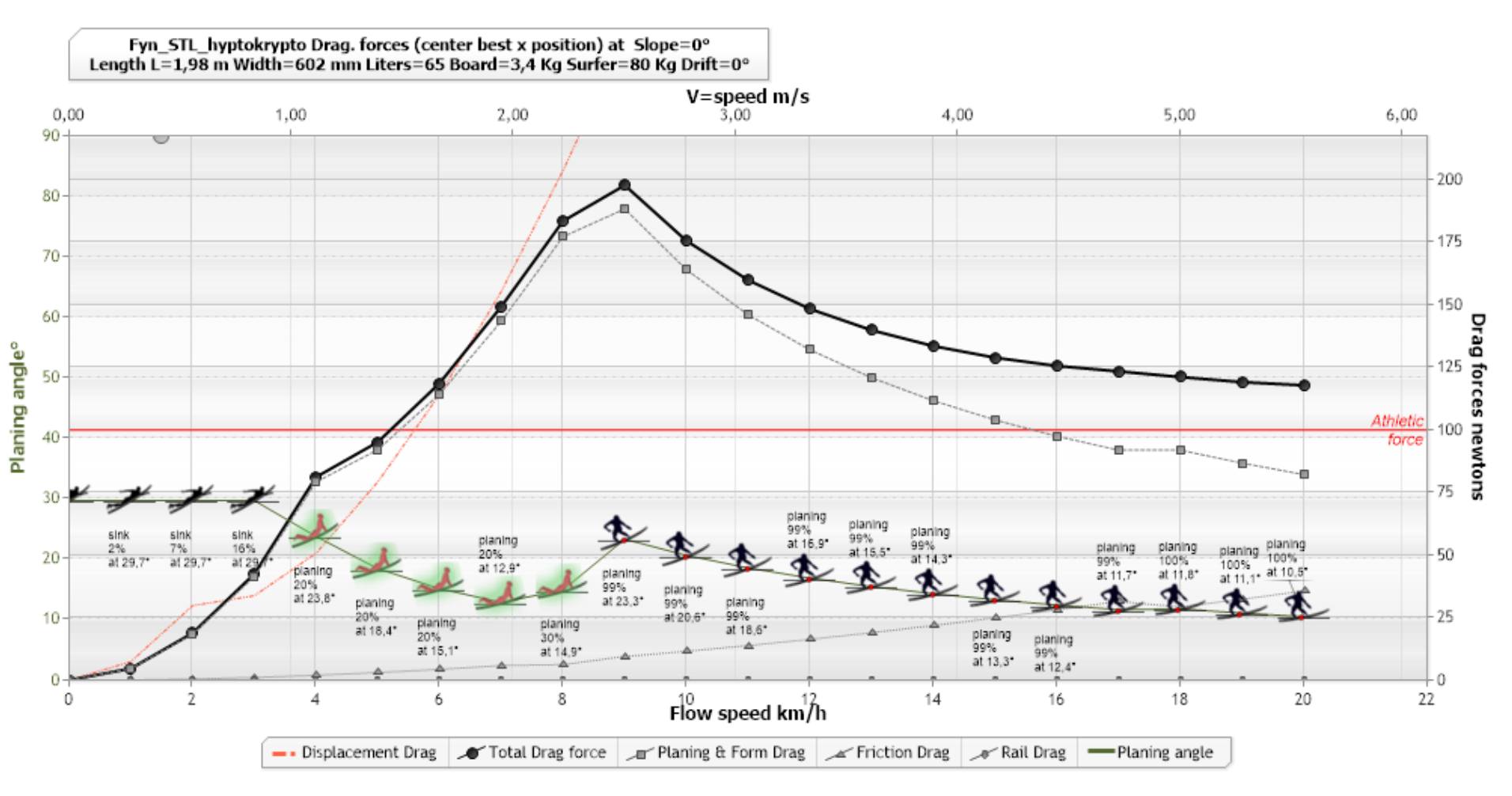
La force de trainée hydrodynamique s'exercant sur une planche de surf resulte en partie de la trainée de friction resulatnt des frottement sur le fond du surf en contact avec l'eau.
La viscosité d’un fluide décrit la force liant ses particules entre elles. Lorsqu’une particule d’un fluide visqueux est mise en mouvement, sa voisine est entraînée par viscosité, et inversement lorsqu’une particule est ralentie, elle freine ses particules voisines. La viscosité de l’eau est faible comparativement à celle de fluides comme le miel, mais elle n’est pas nulle. Lorsque le surfeur prend de la vitesse, les particules d’eau en contact avec la surface de la planche collent à cette surface en entraînant leurs voisines. Si l’on observe les vitesses des particules, en posant comme repère fixe la planche de surf , on constate que les particules au contact direct de la planche sont à l’arrêt et que les particules voisines ont une vitesse qui s’accroît jusqu’à atteindre la vitesse du courant global de fluide. La zone de fluide perturbée par le frottement visqueux est caractérisée par des vitesses inférieures au courant général, cette zone perturbée est la couche limite.

couche limite générant la traînée de frottement (épaisseur exagérée)
Le logiciel shaper wave dynamics integre la trainéee de friction dans l'évaluation de la trainéee hydrodynamique d'une planche de surf (courbe grise triangles, augmantant avec la vitesse)
La couche limite détermine la traînée de frottement visqueux en fonction de la vitesse et de la longueur de la surface en contact avec le fluide. La traînée de frottement varie fortement suivant la turbulence de la couche limite, dans la zone laminaire elle est très faible et dans la zone turbulente elle est plus forte. Le calcul de la force de traînée de frottements est donc divisé en 2 parties, la couche laminaire et la couche turbulente. L’objectif ici n’est pas de détailler ces méthodes de calculs nous utiliserons le logiciel Mecaflux pour établir une évaluation pour différentes vitesses des :
- Traînées de frottements générée par les parties laminaire et turbulente
- Distance du point critique déterminant le passage du régime laminaire a turbulent,
- Épaisseur de la couche limite en bout de planche (utile pour constater l’influence de la couche limite sur les ailerons)
Voici une série de calculs effectués dans une plage de vitesses, allant de la rame, 0.8 m/sec, jusqu’à une phase rapide de 6 m/sec correspondant à des vitesses de vagues supérieures à 2 mètres. Nous prendrons pour exemple une surface de long Board, de largeur 0.6 mètres avec une longueur de partie immergée de 2 mètres dont nous estimerons très approximativement la surface mouillée à 0.6*2=1.2 m²

évolution de l'épaisseur de couche limite et de la distance de point critique en fonction de la vitesse relative
L’épaisseur de couche limite (ligne bleue) varie faiblement et décroit avec la vitesse, elle est de 30 mm environ en bout de planche. Cette diminution, meme faible, d’épaisseur avec la vitesse peut paraître étrange, elle est illustrée dans cette expérimentation aérodynamique ou l’on voit que la couche limite turbulente a vitesse élevée, épouse le profil et décolle plus tardivement que la couche laminaire.

comparaisons couche limites turbulentes et laminaires (Renou, s.d.)

évolution de la traînée de frottements pour une surface de 0.6m de large et 2m de long en fonction de la vitesse.
La traînée de frottement de la surface de notre long Board de 1.2 m² évolue donc de 1.3 à 64 newtons, elle est principalement générée par la zone turbulente de la couche limite. Le point critique de transition de la zone laminaire à turbulente, gagne à être repoussé au plus loin. Cette distance est fortement impactée par la rugosité et les défauts de surface pouvant initier ce décollement prématurément. Une surface très lisse et sans rayures est précieuse dans la partie avant de la planche. Ensuite lorsque la couche limite est décollée, la rugosité perd de son impact.
Nous allons profiter de cette analyse numérique de la couche limite avec le logiciel Mecaflux (MECAFLUX SOFTWARES, s.d.) pour observer l’impact du ratio largeur/longueur sur la couche limite et la traînée de friction. Nous reprendrons les ratios utilisés par Lindsay Lord dans son analyse expérimentale des coques planantes (LORD, 1946).

Le choix de cette référence expérimentale s’inscrit dans notre démarche intégrant l’expérience et le travail des shapers et surfeurs qui ont nous ont légué le surf tel que nous le connaissons aujourd’hui. Bob Simmons est une référence dans l’histoire du shape, en s’inspirant des travaux scientifiques et expérimentaux de Lindsay Lord dans « naval Architecture Of the Planing Hull » et d’autres références aérodynamiques d’après-guerre, il a appliqué un raisonnement scientifique et expérimental permettant des évolutions majeures dans le surf. Il est souvent mentionné pour être l’inventeur du multi fin, mais son travail sur le rôle du ratio de surface, documenté par Lindsay Lord, et son travail sur le profil du rail, s’inspirant des travaux aérodynamiques publiés dans « théorie of the Wing section » est à la base des formes de planches actuelles. Ses travaux ont cependant pris 20 années après sa disparition (1954) pour être appliqués dans les formes de planches du marché. Le multi-fins était un moyen d’apporter plus d’appui au rail, à une époque où le single fin était très court et pouvait « ventiler » dans les phases verticales. Nous verrons plus loin, dans le chapitre sur les ailerons, comment Greenought régla ce problème tout en conservant un single fin. Voici donc les ratios et dimensions de référence expérimentales que nous utiliserons pour accorder notre démarche avec les travaux de nos prédécesseurs.
Voici donc les ratios et dimensions de référence expérimentales que nous utiliserons pour accorder notre démarche avec les travaux de nos prédécesseurs.
Dimensions calculs mecaflux 1 : Largeur x Longueur plaque au repos |
0.49*2.45= 1.2m² |
0.6*2= 1.2m² |
0.69*1.73 = 1.2 m² |
0.77*1.55= 1.2m² |
0.85*1.41= 1.2 m² |
Ratio= Largeur/ Longueur |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
Calculs mecaflux 1 : variation épaisseur couche limite, et variation de traînée de friction en fonction de la vitesse pour divers ratios d’une même surface. L’épaisseur de la couche limite augmente assez proportionnellement à la longueur de la planche. La traînée de frottement augmente elle aussi en fonction de la longueur, mais dans des proportions très faibles qui ne suivent pas l’augmentation de l’épaisseur de couche limite.

évolution épaisseur de couche limite en bout de planche en fonction des vitesses et ratios ( logiciel Mecaflux)

évolution de la traînée de friction en fonction du ratio Largeur/Longueur planche et de la vitesse. Ce graphique montre que la traînée de friction évolue avec la vitesse mais qu’elle est faiblement impactée par le ratio Largeur / Longueur.
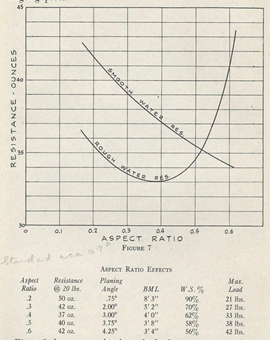
Mesures de traînées globales de plaques planes de divers ratios (LORD, 1946)
Pourtant Lindsay Lord montre dans ses expérimentations que la traînée globale (frottements + traînée de forme aussi nommée traînée de pression) est fortement impactée par ce ratio. Il observe que, en eau lisse, les planches larges (ratio 0.6) génèrent moins de traînée globale que les planches étroites (ratio 0.2). Notons au passage que la tendance de diminution de traînée s’inverse lorsque l’eau devient clapoteuse : une planche large semble plus sensible aux clapots et perd son avantage lorsque la surface de l’eau est perturbée. Le compromis polyvalent étant autour de 0.5. Ce ratio de 0.5 est repris par Ryan Burch en 2009 dans un pain de mousse découpé simplement revêtu d’un enduit noir, pour montrer comment la plus simple des formes possédant un ratio optimal, est capable de vitesse et de manœuvrabilité :

Ryan Burch 2009 Planche ratio 0.5 Lindsay Lord Planning Hull (Kenvin, s.d.)
Dans son ouvrage (LORD, 1946) Lindsay Lord prend soins de nous donner, en plus du ratio, la surface mouillée variant suivant l’angle de planing observé dans ses expérimentations. Il nous fait observer que le ratio de surface modifie l’angle de planing (Pla-ning angle dans graphique précèdent) pour une charge donnée, et que cet angle de planing modifie la surface mouillée (W.S.% dans graphique précédent) dont la réduction diminue la traînée de friction.
Ratio= Largeur/ Longueur |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
Dimensions calculs mecaflux 1: Largeur x Longueur plaque |
0.49*2.45 = 1.2m² |
0.6*2 = 1.2m² |
0.69*1.73 = 1.2 m² |
0.77*1.55 = 1.2m² |
0.85*1.41= 1.2 m² |
Surface mouillée observée d’après (LORD, 1946) |
90%=1.08m² |
70%=0.84 m² |
62%=0.74 m² |
58%=0.69m² |
56%=0.67 m² |
Dimensions calculs mecaflux 2 : Largeur x Longueur mouillée |
0.49*2.20= 1.08m² |
0.6*1.4= 0.84m² |
0.69*1.07= 0.74 m² |
0.77*0.89= 0.69m² |
0.85*0.78= 0.67 m² |
Traînée (approximative en Newton) observée pour une charge (déplacement) de 9 kg d’après (LORD, 1946) |
14,17 |
11,90 |
10,478 |
11,33 |
11,90 |
En effectuant de nouveau les calculs de traînée de friction pour les divers ratios, mais en intégrant une surface mouillée modifiée suivant es observations de Lindsay Lord, on met en évidence que la traînée de friction diminue avec la surface mouillée.

Nous pouvons cependant remarquer que la plus faible traînée observée par Lindsay Lord est au niveau du ratio 0.4 alors que les calculs désignent le ratio 0.6 comme étant le moins énergivore en termes de friction. Cette différence s’explique par l’augmentation de traînée de forme générée par l’augmentation de la surface frontale opposée au flux, causé par l’augmentation de l’angle d’incidence observé pour un centre de gravité fixe. Ceci n’a bien sûr pas échappé à Lindsay lord qui préconise un déplacement du centre de gravité vers l’avant pour rétablir une assiette diminuant la surface frontal et l’angle d’incidence. Ceci n’échappe pas non plus à l’intuition du surfeur qui recherche la meilleure position de rame, ou le marin qui se déplace vers l’avant de son annexe pour la faire déjauger. Mais au-delà de certaines vitesses, nous verrons que la friction devient prépondérante et que le placement gagne a revenir sur l’arrière pour diminuer la surface de friction.
Nous conclurons donc notre réflexion sur l’impact de la traînée de friction et du ratio de surface par le constat suivant :
• La largeur est un facteur de performance en termes de réduction de traînée de friction car elle diminue la surface mouillée au planing.
• Cet apport devient moins conséquent à partir du ratio 0.5 et même contre-productif dans des conditions de clapots.
• Une importante largeur sera pleinement exploitée en déplaçant le centre de gravité sur l’avant pour rétablir un angle d’incidence faible, il en résulte une position de wide point pensée pour cette accélération par appui avant.
Nous ajouterons que cet exercice d'estimation de la traînée de friction aurais pu être largement simplifié avec le logiciel ShaperWaveDynamics, qui établit l'angle de planing optimal et la surface mouillée pour produire les graphiques de traînée de friction+traînée de forme en fonction d'une planche donnée: Voir: Traînée hydrodynamique surf