Surfers expérimentés ou débutants, prof d’école de surf ou shaper, nous avons tous intérêt à bien comprendre quelles sont les conditions à réunir pour qu'un take off soit possible: Ce qui nous intéresse ici est l'aspect physique du surf, et plus particulierement celle du take off, nous ne détaillerons donc pas ici la pédagogie du take off, une recherche "apprendre take off surf" sur le net donne de très bons cours à ce sujet. Du point de vue du surfer, le take off est l'instant ou il se redresse sur sa planche, pour prendre le contrôle de sa trajectoire en position debout. Mais se relever sur la planche ne suffit pas, il faut que ceci soit fait au bon endroit et au bon moment.

take off surf

Plus le surfer est expérimenté, plus il maitrise un enchaînement de gestes répétés qui se transforment en réflexe. Cet instinct, renforcé par l’expérience, englobe sans les distinguer les diverses conditions spécifiques nécessaires au take off, comme une sensation, permettant ce take off. Nous pensons: ça va le faire, et Action! Si ça le fait, parfait! Pourquoi creuser davantage?

Mais si ça le fait pas?, ou si le surfer veut améliorer sont take off?, ou bien simplement expliquer au shaper ce qu'il faudrait améliorer sur la planche ? Il devient alors utile de creuser un peu, sous l'instinct, pour trouver des arguments compréhensibles et partageables. Nous définirons donc ici le take off, non pas comme une action du surfer, mais comme le somme des conditions le rendant possible. Car c'est en décrivant et comprenant bien chacune de ces conditions nécessaires, que nous pouvons améliorer notre take-off, ou la planche.

Les arguments numériques, sont fournis ici dans un soucis de transparence, mais le lecteur peut très bien survoler les formules qu'il trouve rébarbatives, et prendre simplement connaissance des conclusions qui lui seront utiles dans sa recherche d'optimisation de son take off ou de sa planche.

Les 3 conditions du take off:

  1. La vitesse: Pas de choix, ce paramètre dépend de la vague! Prendre une vague c'est attraper le train en marche! Le surfer doit atteindre la vitesse de crête imposée par la vague: Si le surfer se déplace à une vitesse inférieure à la celle de la vague, lorsque la crête arrive à son niveau, il sera dépassé par la vague. C'est une évidence, mais nous verrons plus loin qu'obtenir cette vitesse relève d'une stratégie, savamment élaborée par le shaper, en fonction du surfer et la vague.
  2. Le placement: Le placement du surfer est relatif au peak. Le surfer doit repérer ou le peak va apparaître en observant la vague, et être capable de le montrer du doigt bien avant qu'il ne déferle. C'est un point géographique fixe, le surfer peu s'aider de repères terrestres (voir "alignements navigation"). Mais la position du peak n'est qu'un repère, attendre la vague au peak est une très mauvaise idée! Lorsque le peak arrive, le surfer doit déjà avoir acquis la vitesse de vague, et avoir déjà réalisé son take off. Pour un surfer seul sur le spot, Le placement consiste à estimer la distance de rame nécessaire pour atteindre la vitesse de crête, avant que le peak ne soit atteint. le surfer devra donc se placer au large du peak, à une distance légèrement plus grande que celle néccéssaire pour la prise de vitesse. Nous reviendrons en détail sur les différentes stratégies qui s'offrent au surfer pour choisir cette distance nécessaire.

    (Détail interface Analyse take off, du logiciel ShaperWaveDynamics)

  3. Le moment: la pente du take off: Le moment du take off est lui aussi relatif au peak. Admettons pour notre propos, que le déferlement du peak s’amorce lorsque la face de vague atteint une pente maximale avoisinant 60 degrés. Le surfer devra donc avoir atteint la vitesse de crête, avant que la pente n'atteigne 60 degrés. Le moment du take off doit être le plus en avance possible sur cet instant ou la pente franchie les 60 degrés. Si le surfer se redresse après 60 degrés, le (late) take off sera très technique voir impossible, par contre, si le take off est réalisé avant 60 degrés, le surfer pourra choisir sa trajectoire avec plus de liberté. Remarquez que nous prenons ici le soins de remplacer la notion de temps, par la notion géométrique de pente. (voir pensée géométrique du surf) Nous pouvons dire que, plus la pente est faible au moment du take off, plus le surfer aura d’espace et de choix pour ajuster sa trajectoire avant le déferlement (60°). Le shaper notera qu'une planche apportera plus de liberté et d'aisance si elle favorise le take off à faible pente. Le shaper à grand intérêt à maîtriser ce paramètre, que nous détaillerons donc plus loin. Mais voyons un autre point essentiel qui relie la période et la variation de la pente:

    :

    4. (Détail interface Analyse take off, du logiciel ShaperWaveDynamics)

    La pente d'une vague varie suivant un cycle d'une période (prenons par exemple 12 secondes), elle passe donc d'une pente de zéro en position basse, à une pente de zéro en position haute, durant 1/2 période (6 s) , et l'on peu estimer qu'elle passe de zéro a 60 degrés, en phase montante en 1/4 de période (3 s). Cette estimation est largement assez précise pour le sujet qui nous intéresse: Nous pouvons estimer qu'un surfer, positionné au peak sans bouger, voit la vague passer de 0 a 60 degrés en 1/4 de période(3s). C'est en fait le temps durant le quel le surfer sera exposé à une composante propulsive de la pente, si il ne bouge pas. Remarquerons simplement ici, que le surfer est exposé moins longtemps à la pente propulsive dans une vague de courte période, que dans une vague de longue période, nous verrons plus loin ce que cela implique...

Pour résumer, les 3 conditions "limites", minimales du take off sont:

  1. Vitesse surfer = vitesse crête. lorsque le surfer atteint la vitesse de crête, il réalise le take off.
  2. Placement surfer=Distance nécessaire pour atteindre la vitesse crête. Si la vitesse de crête est atteinte avant le peak, c'est un avantage qui donne un atout au surfer
  3. La pente du take off=Redressement avant 60 degrés de pente. Plus la pente de take off est faible, plus surfer à de la liberté et de l'avance, sur la vague et les éventuels concurrents. Mais notons une limite a cela: le concept de Pente minimale propulsive: La planche est soumise à une force de résistance à l'avancement, nommée traînée, qui s'oppose et diminue la force de propulsion "utile". La force de propulsion utile, Fpu, est donc: Fpu= Fp-trainée. Si Fpu<0, la planche ralenti. Quand le surfer ne rame plus, la force de propulsion, Fp, est produite uniquement par la pente. Il est donc prématuré de ce redresser sur une pente qui ne produit pas un force de propulsion utile >0. Nous nommerons Pente minimale propulsive, la pente qui produit une force propulsive supérieure à la traînée, donc une force de propulsion utile supérieure a zéro, pour un surfer et une planche donnée, à une vitesse donnée. La pente idéale de take off, en terme d'avance sur le déferlement, et les éventuels concurrents, ne sera jamais inférieure à la pente minimale, mais le plus proche possible.

Reprenons maintenant ces conditions en détails et voyons ce qu'elles impliquent:

La condition de vitesse:

  • La vitesse de la vague (en eau peu profonde) est donnée par la formule C= racine(9.81/Profondeur). Ceci implique qu'une vague déferlant sur un fond de 3 mètres est plus rapide qu'une vague déferlant sur un fond de 1 mètre. Retenons bien que, la vitesse de la vague dépend uniquement et simplement de la profondeur à l'endroit du peak, et que nous n'avons aucun levier pour modifier ce fait. Nous devons produire cette vitesse d'une manière ou d'une autre, sinon pas de vague!
  • Accélération: Atteindre la vitesse signifie accroître la vitesse du surfer, de zéro à la vitesse de crête. Ceci est formulé en physique, par la notion d’Accélération: a=(Vc-V0)/dt, avec a = accélération en m/s², V0=vitesse initiale m/s, Vc = vitesse crête m/s, et dt=intervalle de temps en secondes, durant le quel la vitesse passe de v0 aVc. Exemple: Passer de 0 a 3.1 m/s en une seconde (vitesse d'une vague de 1m) , consiste à accélérer de a= (3.1-0)/1= 3.1 m/s². Si l'on dispose de 2 secondes pour effectuer cette variation de vitesse, l’accélération est d'autant plus faible: A= (3.1-0)/2= 1.55 m/s². Notons bien que, plus on dispose de temps pour atteindre un vitesse donnée, moins nous avons besoin d’accélérer.
  • Source propulsive: Pour obtenir la vitesse , le surfer utilise donc une force propulsive, Fp, pouvant venir de diverses sources:
    • Force musculaire de rame: Un surfer puissant produit environ 140 newton (valeur très variable en fonction du surfer et de sa condition)
    • Projection de la portance de la planche: ce résultat dépend de la pente et du poids du surfer
    • traction de voile, jet ski, moteur + hélice...

      Fp= somme des forces de propulsions.

  • Résistance propulsive: la planche est malheureusement soumise à une force de résistance à l'avancement, nommée traînée, qui s'oppose et diminue la force de propulsion. Cette force de traînée hydrodynamique évolue en fonction du carré de la vitesse, et dépend fortement du poids, de l'incidence et de la forme de planche. Nous y revendrons, et retiendrons simplement ici que la traînée hydrodynamique diminue la force de propulsion.
  • Force de propulsion utile: la planche est donc soumise à une force de résistance à l'avancement, nommée traînée, qui s'oppose et diminue la force propulsion "utile". La force de propulsion utile, Fpu, est donc :

      Fpu= Fp-trainée.

    Cette force propulsive utile procure l’accélération décrite par la loi de Newton: Fpu=m*a. Nous pouvons ainsi estimer la force nécessaire pour accélérer un surfer d'un poids donné.

    exemple: Pour propulser un surfer de 80 kg, à l’arrêt a la vitesse de crête 3.1 m/s (vague 1 mètre), il faut appliquer une force Fpu, de : Fpu=m*a=>Fpu=80*(3.1-0)/1=248 newtons (25 kgf environ). Comme nous l'avons vu plus haut, si nous avons 2 secondes pour effectuer cette accélération la force est diminuée par 2: Fpu=80*(3.1-0)/2=124 newtons (12.5 kgf environ). Nous retiendrons un point très important pour la stratégie du take off: Plus nous disposons de temps pour la prise de vitesse, moins nous avons besoin de force!

Pour résumer, La vitesse, imposée par la vague, impose donc l’accélération. Le poids du surfer et la vitesse de vague, étant des facteurs sur lesquels le surfer n'a aucun pouvoir au moment du take off, les 2 leviers restant à sa disposition pour acquérir la vitesse de vague, sont le temps d'accélération et la force de propulsive.

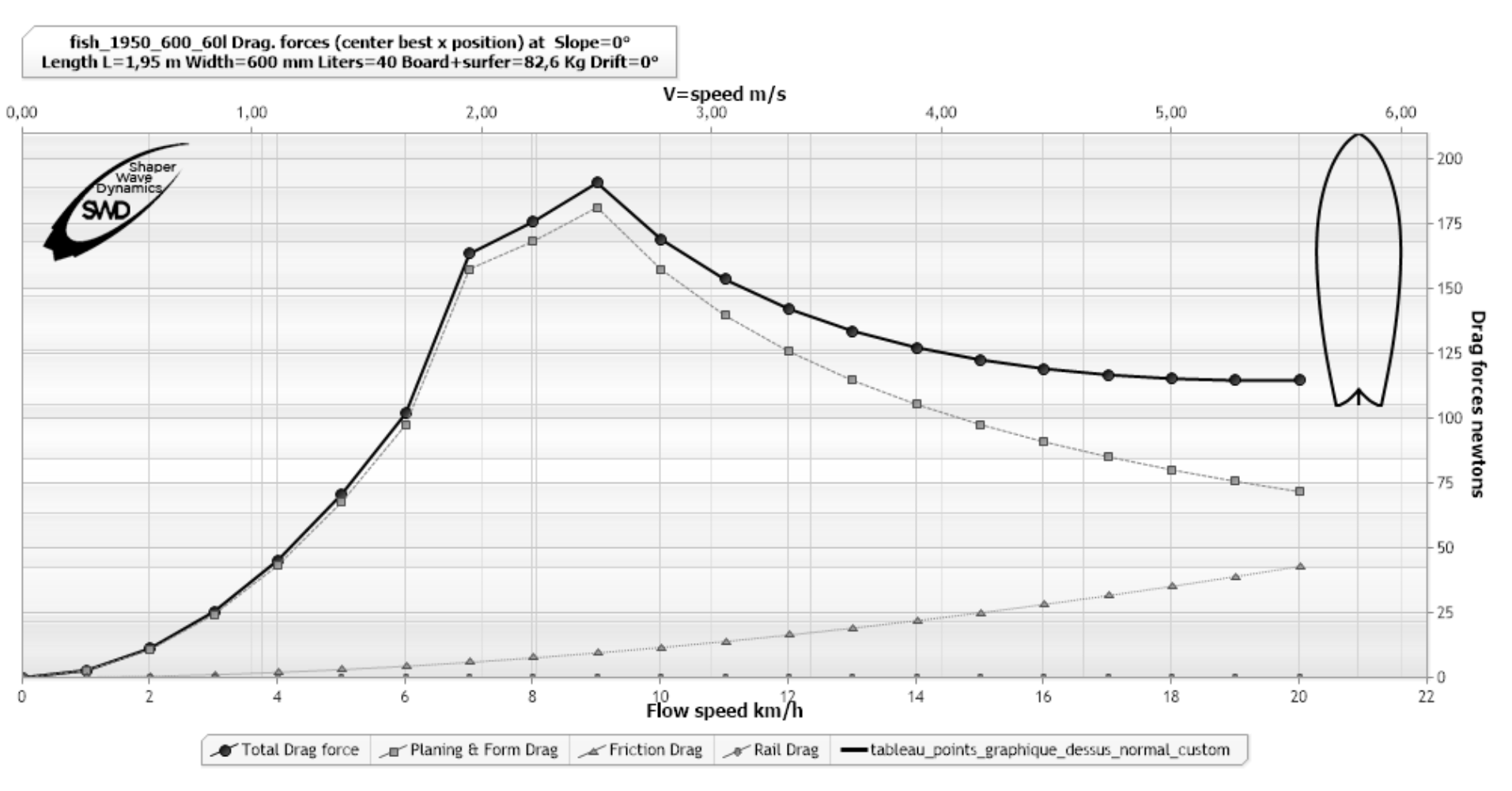
A ce stade nous devons nous accorder sur la définition de la force propulsive: Comme nous l'avons vu plus haut, la force propulsive est contrariée par une force de résistance à l'avancement: la traînée hydrodynamique:surfboard fish

(exemple Analyse traînée hydrodynamique, logiciel ShaperWaveDynamics)

La courbe (points ronds noir) de ce graphique montre la variation de traînée hydrodynamique d'une planche donnée avec un surfer donné, dans une plage de 0 a 22 km/h. Ce graphique montre, par exemple, que la traînée de la planche à 4 km/h est 45 N environs. C'est la force qu'il faut fournir pour conserver la vitesse. Si on applique une force supérieure, on accélère, si on applique une force inférieure, on décélère, si la force propulsive est égale a la force de traînée, la vitesse est constante.

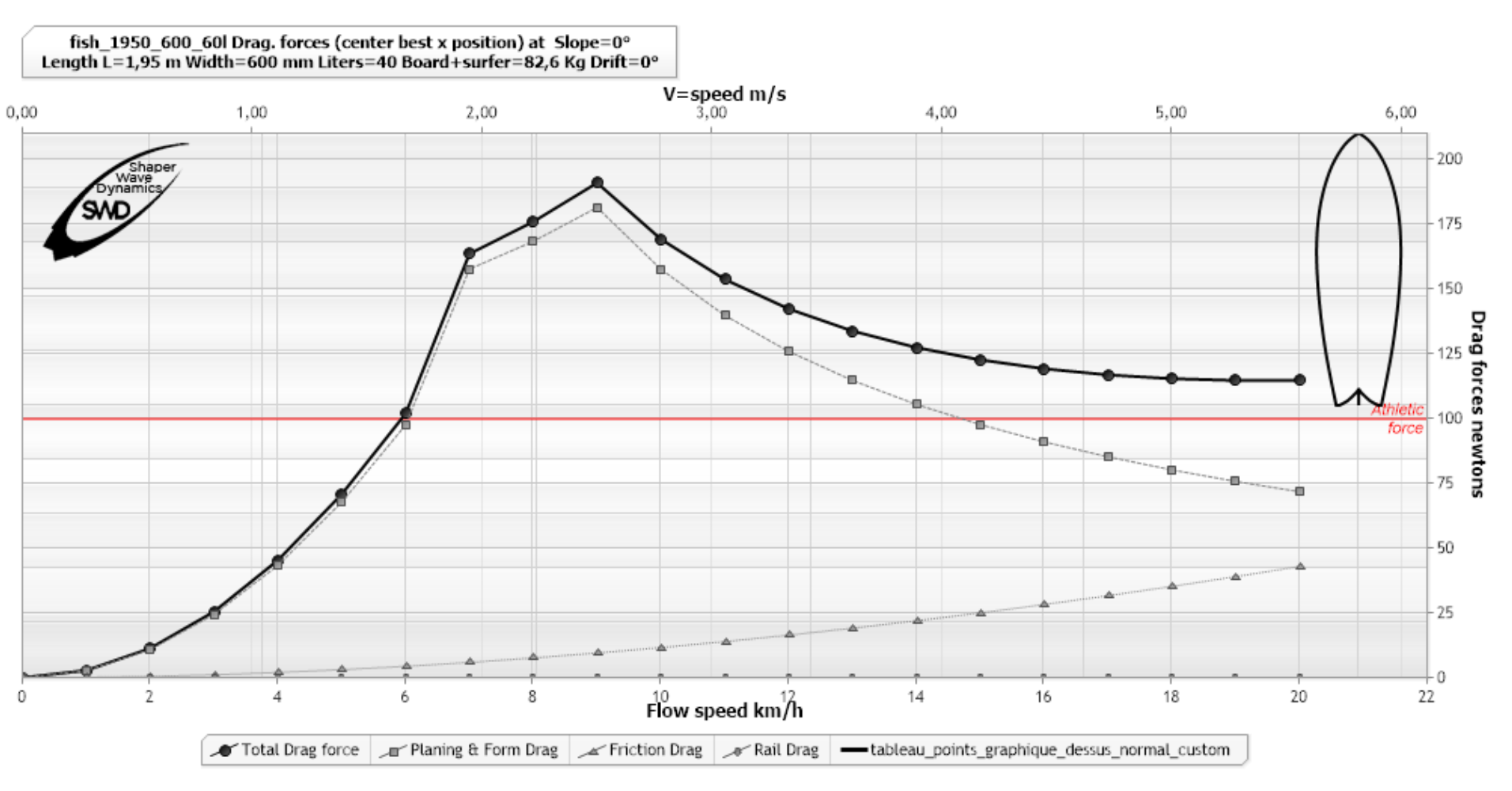
Ajoutons maintenant à ce graphique une ligne horizontale marquant la force de 100 N, qu'un surfer en bonne condition peu fournir raisonnablement:

Si on relève que la force de traînée, a 3 km/h est de 25N, la force propulsive utile a 3 km/h, pour un surfer fournissant 100 N a la rame sera donc 100-30 = 70 newtons. elle ne sera plus que 100-100=0N à 6 km/h et le surfer ne pourra jamais dépasser 6 km/h à la rame sur cette planche car sa traînée serait alors supérieure à la propulsion et empêchera toute augmentation de vitesse. Ce graphique nous indique donc que le surfer produisant 100 N à la rame atteindra une vitesse limite de 6 km/h, correspondant à l'intersection de la courbe de traînée et de la ligne rouge des 100 N. Une planche donnée possède donc une vitesse limite, pour un surfer de poids et force donnée. Nous commençons à percevoir l’intérêt que peut avoir la courbe de traînée hydrodynamique pour le shaper et le surfer...

  • La condition de placement: La question du placement peut se résumer à : Quelle distance faut il pour passer de zéro, à 3.1 m/s? Le surfer répond à cette question empiriquement: En effectuant plusieurs essais, il ajuste sa position à chaque échec, jusqu’à réussir son take-off. Mais nous aimerions découvrir les potentiels leviers théoriques d'amélioration du take off. Les manuels de physique nous donnent une solution au problème classique de distance d'accélération:

    • D = (Vc²-V0²)/(2*a) (réf: kane/sternheim Physique) Avec Vc vitesse crête, V0 vitesse initiale, D= distance à parcourir pour atteindre la vitesse Vc, et a= accélération en m/s².

    Cette formule nous montre que la distance de placement, D, diminue donc lorsque l’accélération, a, augmente.

    L’accélération étant par définition: a= (Vc-V0)/ dt, et la force propulsive utile, Fpu, étant par définition Fpu= m*(Vc-V0)/ dt, nous pouvons reformuler en répartissant d'un coté de l'égalité, les variables que le surfer peut contrôler, et de l'autre les paramètres imposé. En admettant V0=0, nous obtenons: Fpu*dt=m*Vc . Pour information, Le terme physique décrivant Fpu*dt, est l'impulsion. Autrement dit, la force propulsive utile et la durée d'exposition à cette force , forment l'impulsion. L'impulsion est le facteur principal du take off. La formulation Fpu*dt, met en évidence les stratégies offertes au surfer pour fournir une même impulsion:

    1. Stratégie de la durée d'exposition: être exposé un maximum de temps au minimum de force: Cette stratégie permet des take off en avance sur le peak, nous l'étudierons en détail plus loin.
    2. Stratégie de la force propulsive utile: être exposé un minimum de temps au maximum de force: Cette stratégie permet une take off très proche du peak, nous l’étudierons aussi plus loin.

Ces 2 stratégies sont des extrêmes, le surfer dispose d'une possibilités de dosage entre ces 2 extrêmes. L'analyse de ces limites offre une vison de la plage d’utilisation d'une planche donnée, pour un surfer donné, dans une vague donnée. Et c'est bien ce que le surfer et le shaper désire connaitre avant de se lancer sur un achat ou une conception de planche!

Nous pourrions intuitivement penser que la stratégie de la force est réservée aux surfers musclés et puissants, mais ceci n'est pas forcément vrai, du fait des diverses sources propulsives à la disposition du surfer. Nous avons précédemment distingué 3 sources de propulsion:

    1. la force de rame,
    2. la résultante de force de gravité projetée par la pente,
    3. et les forces externes de traction de type voile ou jet ski...

Nous exclurons de notre questionnement les forces externes, pour cibler le cas du surf traditionnel. Il nous reste donc 2 sources, la rame et la gravité.

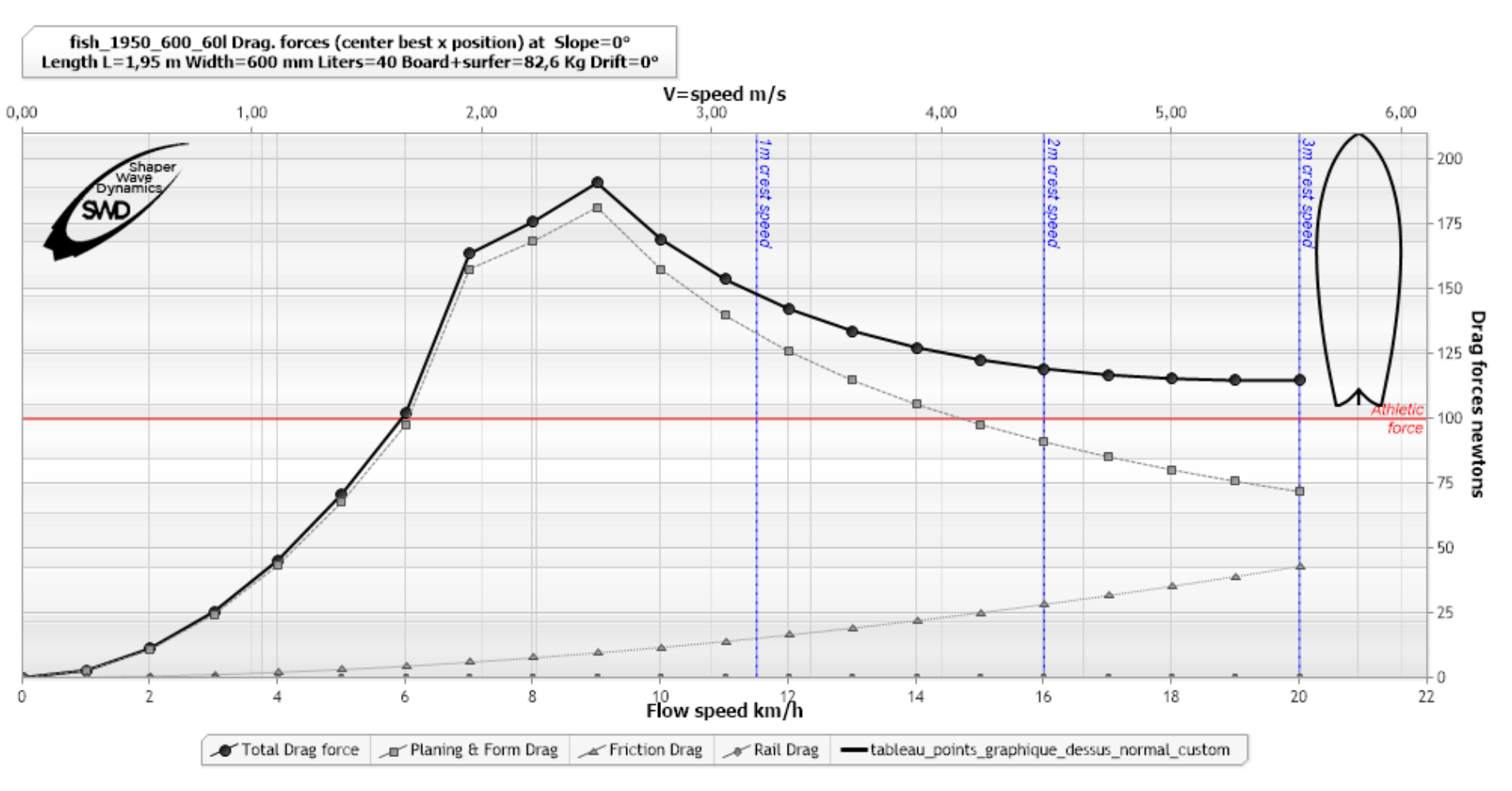
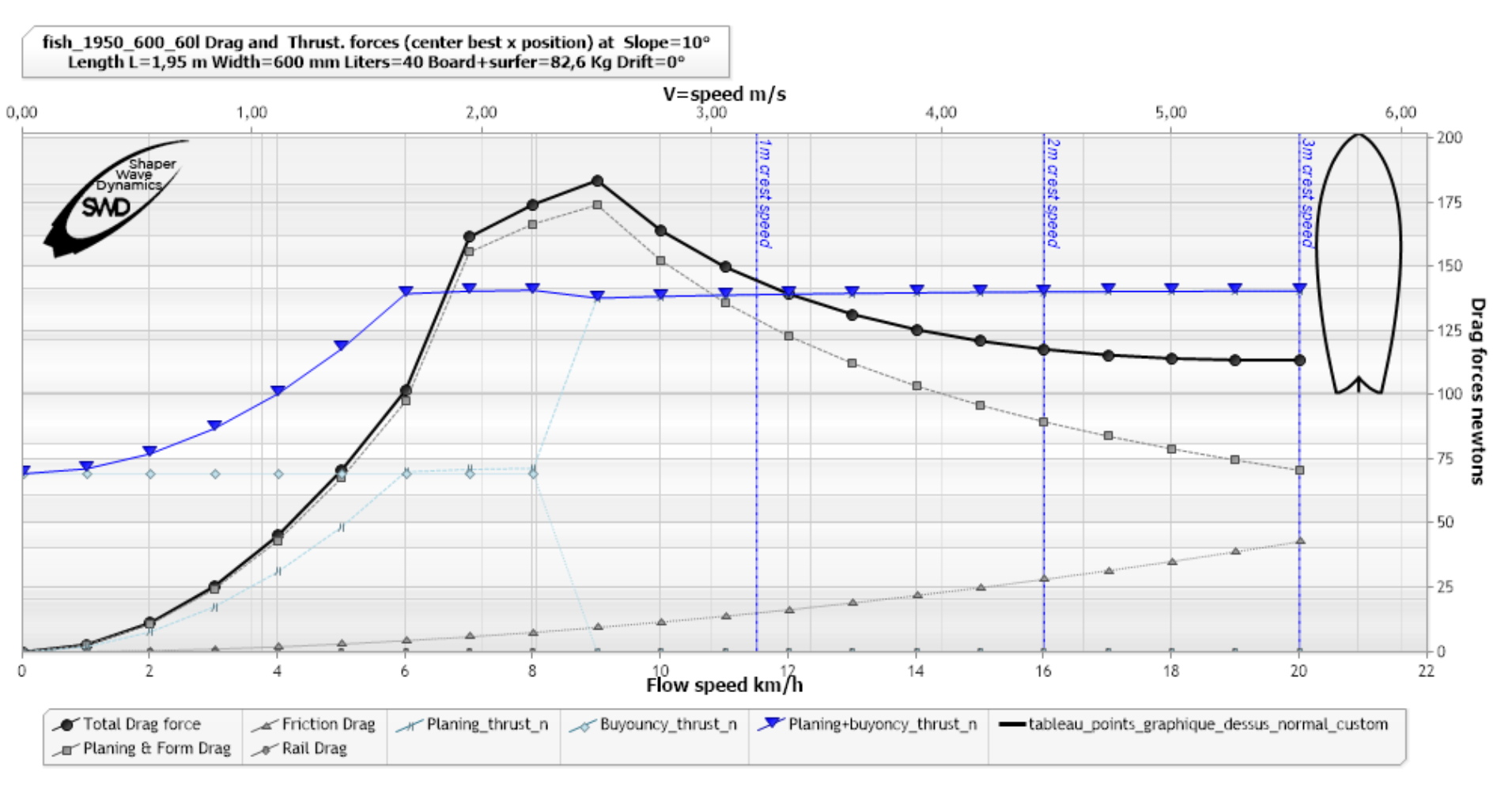
Ajoutons à notre graphique de traînée, 3 marqueurs verticaux, en bleu, qui indiquent respectivement les vitesse de crêtes approximatives, de vague de 1, 2 et 3 mètres, que doit atteindre le surfer pour son take off:

vitesse crtes vagues et trainee planche surf

Pour atteindre les 11.5 km/h de la vague de 1 mètre, nous voyons qu'il faudra dépasser un pic de résistance de 190 N environs. Nous voyons que notre surfer produisant une force de 100N à la rame, sera limité à 6 km/h. Il faut donc au surfer une autre source de propulsion si il veut prendre la vague de 1 mètre: la gravité. Ou plus exactement, la réaction résultant de la vague en contact avec la planche.

Cette poussée gravitaire résultante de la portance (hydrostatique ou hydrodynamique), augmente en fonction de la pente. Voici 2 graphiques inscrivants la poussée résultant de pentes de 10 et 15 degrés pour la même planche et le même surfer:

force propulsive de pente 10 degre de vague

(Poussée courbe triangles bleu) à 10 °, logiciel ShaperWaveDynamics)

Le graphique ci dessus nous montre qu'un surfer exposé suffisamment longtemps à la La pente de 10 degrés, verra sa vitesse augmenter jusqu’’à la limite de 6.5 km/h.

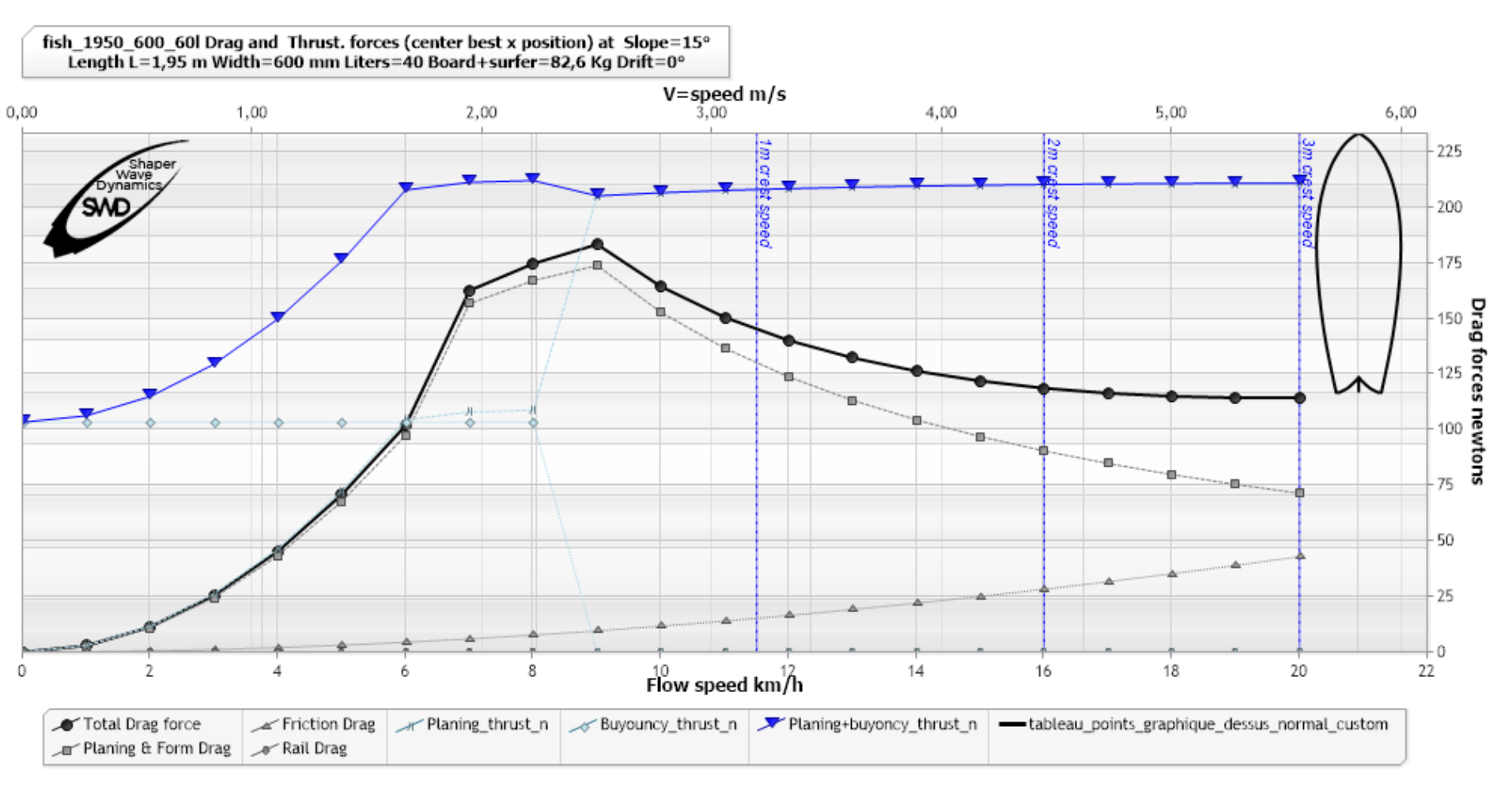
force propulsive de pente 15 degre de vague

(Poussée courbe triangles bleu) à 15 °, logiciel ShaperWaveDynamics)

Le graphique ci dessus nous montre qu'un surfer dans la pente de 15 degrés, à 6 km/h sera soumis à une Force propulsive gravitaire(buoyancy+planing) de 213 N et une force de traînée(drag) de 100 N. La force propulsive utile sera donc de 213-100=113 N. La masse du surfer+planche étant de 82.6kg dans cet exemple, L'accélération a 6km/h de ce surfer sur cette planche, à 15 degrés de pente est donc de : F=m*a => 113/82.6=1.36 m/s².

Voici le même graphique avec l'accélération:

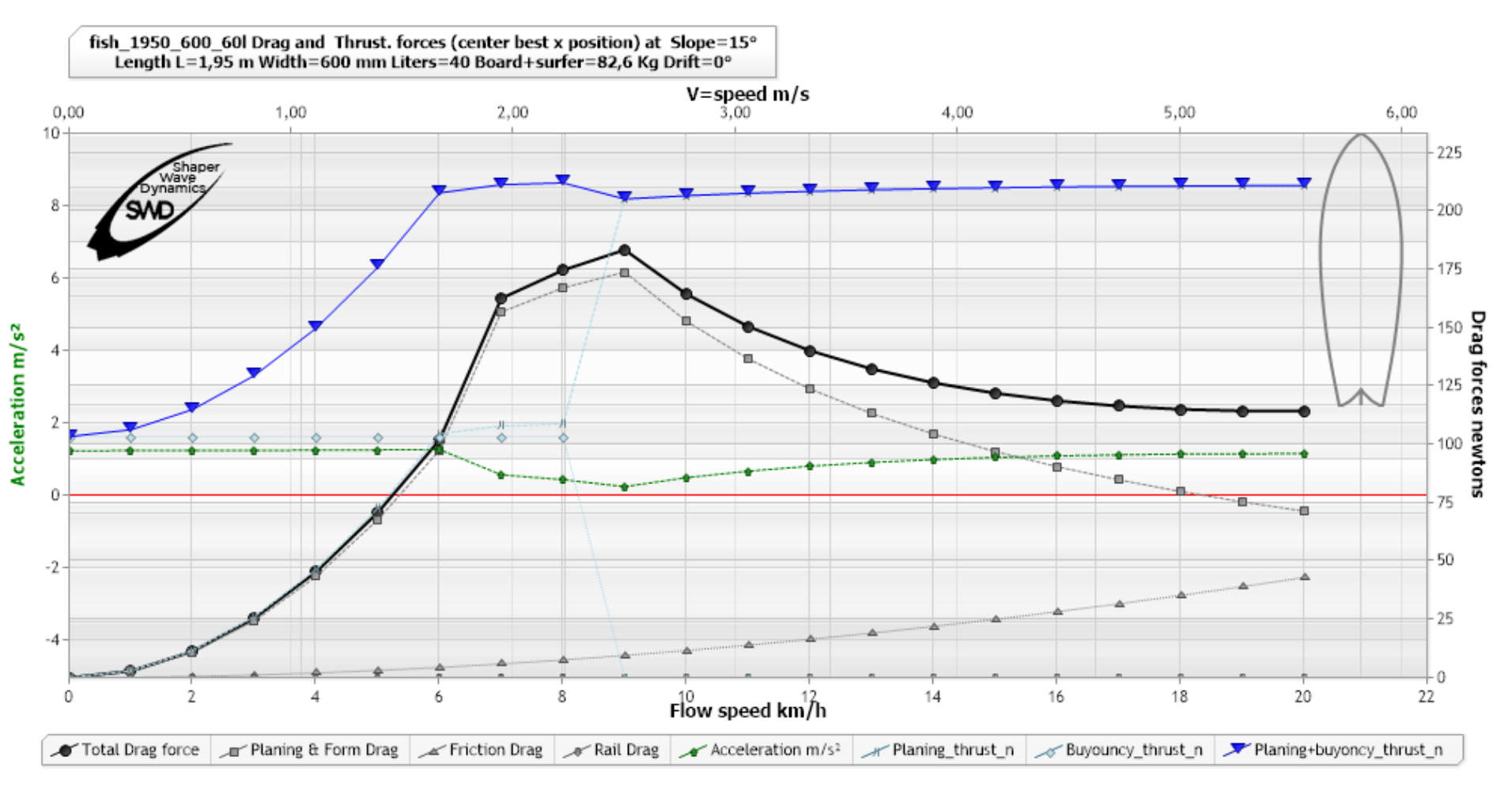
acceleration surf pente 15 degres

(Accélération courbe verte pointillés points flèches) à 15 °, logiciel ShaperWaveDynamics)

et l’accélération pour la pente de 10 degrés ou nous voyons une zone de décélération entre 7 et 12 km/h:

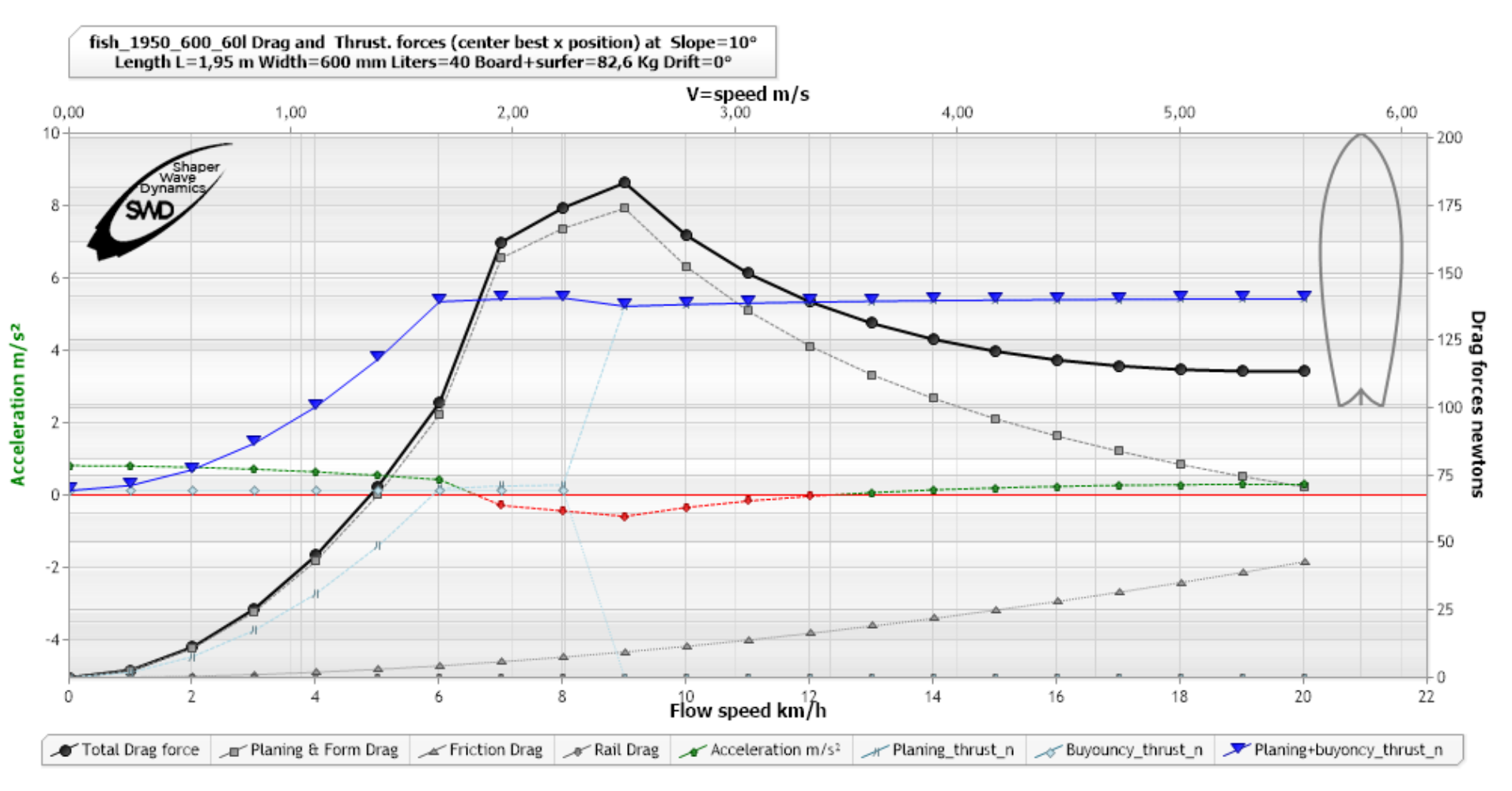
acceleration surf pente 10 degres

(Accélération courbe verte pointillés points fléchés) à 10 °, logiciel ShaperWaveDynamics)

En fait le surfer va être exposé a une pente donnée, durant un temps donné seulement. Ensuite la pente va changer, évoluant ainsi de zéro a 60 degrés. Le surfer sera donc exposé, durant un moment dT, à 1 degré, ensuite à 2 degrés, ensuite à 3 degrés, ensuite ...OK j’arrête. En réalité ce changement est continu et progressif, mais nous pouvons estimer que si nous connaissons la durée de variation de la pente, dT, pour 1 degré, et l’accélération à ce degré de pente, nous pouvons obtenir la variation de vitesse dV, produite à chaque degré:

dV=a*dT

Cette durée dT nous l'avons en fait déjà définie plus haut lorsque nous avons lié la pente à la période: Nous savons que notre pente évolue de 0 a 60 degrés en 1/4 de période.(Pour être plus précis nous devrions utiliser une réglé de variation basée sur le sinus de l'angle, mais restons dans une approximation linéaire, qui sera largement suffisante entre 0 et 60 degrés.) La durée de variation de 1 degré est donc de:

dT=période/4/60=période/ 240.

Prenons un surfer+planche de masse 82.6 kg, positionné à la pente 0 degrés légèrement au large du peak, d'une vague de période 12 secondes déferlant sur un fond de 1 mètre (nous estimons que la hauteur de vague et la profondeur au peak sont équivalentes), à la vitesse de 3.1 m/s.

(Détails interface Analyse take off, du logiciel ShaperWaveDynamics)

S'il ne bouge pas, le surfer verra la pente évoluer de zéro a 60 degrés en 3 secondes.

  • Remarque: Nous pouvons ainsi évaluer à quelle distance se trouve la pente 60° (déferlement) lorsque nous percevons un certain angle de pente à notre position, en utilisant la vitesse de crête: par exemple Distance de la pente 60° lorsque le surfer est à la pente 0°=3*3.1=9.3 mètres. Nous utilisons intuitivement ce type d'estimation de la pente lorsque nous ramons, et devinons sans nous retourner, si le peak est plus ou moins proche, en fonction de la pente ressentie.

le laps de temps, dT, pour augmenter de 1°, la pente de notre vague de 12 secondes de période, est donc: dT=période/ 240=0.05 secondes

Observons l évolution de la vitesse du surfer à chaque degrés de pente: V0°, V1°,V2°,V3°,V4°....:

Partant à vitesse nulle, à 0° degré, le surfer ne recevra aucune force propulsive gravitaire, et il devra donc ramer pour générer de l'accélération. En admettant qu'il produise une force propulsive 100 N à la rame, et que à l’arrêt il ne rencontre pas de résistance à l'avancement, son accélération sera alors F=m*a => a=100/82.6=1.21 m/s². Nous pouvons dire que sa vitesse va évoluer de V0° à V1° durant un intervalle dT=0.05s, suivant V1°=V0°+(1.21*0.05)=0.06 m/sec.

Le surfer se trouve désormais sur une pente de 1°, avec une vitesse non nulle...

Une petite finesse, qui plaira aux surfers sensibles à la distorsion temporelle ressentie pendant le surf, doit être maintenant ajouté à notre calcul: Le temps de variation par degrés, dT, est modifié par la vitesse du surfer: En effet, si le surfer se déplace à la même vitesse que la vague, il ne percevra pas de variation de la pente, car il l'accompagne. C'est d’ailleurs ici que réside la sensation de surf: le surfer suit un événement "atemporel" dans un repère purement géométrique, dont la référence est la pente. Une vague qui ouvre est une vague ou le surfer perçoit une pente constante qu'il peut suivre. Cette aspect géométrique subjectif du surf est plus largement développé sur la page pensée géométrique.

Si le surfer est en mouvement , nous devons donc tenir compte de "l'étirement" de la durée de variation de pente, dT, produit par la vitesse "d'accompagnement" de la vague. Nous introduisons donc un facteur d'accompagnement, aV, qui tend à accroître dT lorsque la vitesse du surfer, Vs, augmente. aV tend vers l'infini lorsque Vs atteint la vitesse de vague, et tend vers 1 lorsque Vs = 0: Nous définissons donc le Facteur d'accompagnement aV=Vc / (Vc - Vs), dans la limite Vs<Vc et devons reformuler notre intervalle : dT = période/ 240 * aV

Nous passons donc d'une vitesse à une pente n°, à une vitesse à la pente suivante n°+1 d’après la formule:

Vn°=Vn°-1+(an°*(période/ 240) * (Vc / (Vc - Vn°-1))

avec an°, l'accélération calculée à la pente n° suivant : Fpun°=m*an° => an°= Fpun-1°/masse_kg , avec Fpun° la force propulsive utile à la pente n°-1 en fonction de la vitesse Vn°-1

Lorsque Vn° atteint la vitesse de crête nous avons résolu la pente de take off minimale pour le surfer et la planche donnée:

(Rampe d'accélération en fonction de la pente), logiciel ShaperWaveDynamics)

Ce graphique montre l’évolution des forces propulsives utile, de l’accélération, de la vitesse et l’étirement de la durée de pente par secondes, pour une planche et un poids de surfeur donné. Le surfer atteindra la vitesse de Vague de 1 mètre (3.1ms), lorsque la pente sera de 30 degrés. En connaissant l'évolution des vitesses, nous pouvons positionner le surfer à chaque point de la rampe d'accélération et déterminer la distance parcourue. Voici un schéma indiquant pour un surfer donné, sur une planche donnée, dans une vague donnée, en considérant que le surfer réalise le take off lorsqu'il atteint la vitesse de vague:

  • la distance parcourue pour rejoindre la vague en partant d'une pente et d'une vitesse nulle
  • le temps pour rejoindre la vague en partant d'une pente et d'une vitesse nulle.
  • La distance restante avant déferlement, lorsque le surfer est en position de take off
  • La distance restante et le temps avant déferlement, lorsque le surfer est en position de take off

 

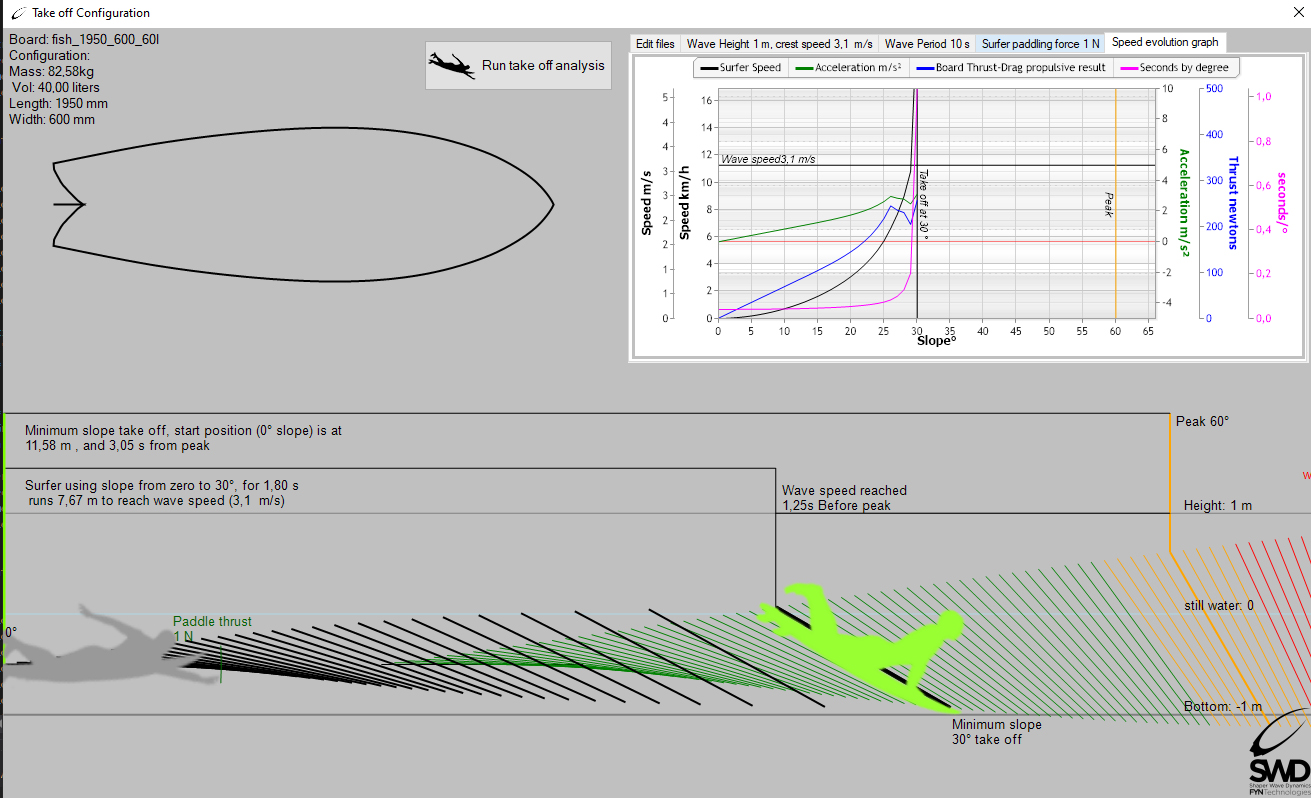
analyse take off surf

(Analyse take off, logiciel ShaperWaveDynamics)

Le placement est donc décrit par une distance, mais il conditionne aussi la pente à laquelle le take off pourra être réalisé avec une planche donnée. Cette analyse avec un take off sur pente minimale, décrit la stratégie d'exposition maximale a la pente avec le minimum d'effort. C'est celle qui procure au surfer la possibilité de se lever le plus tôt. C'est en testant diverses hypothèses de formes, avec cet outil logiciel, (Analyse take off, logiciel ShaperWaveDynamics), que le shaper et le surfer pourront évaluer si leur projet de planche est meilleur qu'un autre en comparant les angles minimum de take off, avant de se lancer dans la réalisation de la planche.

Voyons la stratégie avec effort maximum et durée d'exposition minimale:

Nous avons calculé précédemment, la pente minimale de take off, en initialisant notre calcul avec un surfer placé sur la pente 0°. Nous avons vu que la force propulsive devait être positive pour commencer à se déplacer.

Le surfer peut rester assis sur sa planche, sans ramer, de sorte à créer une résistance à l'avancement maximale, neutralisant la force propulsive gravitaire, et laisser ainsi la pente augmenter, sans être propulsé, ni déplacé.

Le surfer peut ainsi attendre, et choisir de s'allonger en position de traînée minimale,à une pente plus importante pour commencer sa rampe d'accélération.

Nous pouvons évaluer la pente de départ maximale, qui génère une rampe d'accélération permettant d'atteindre la vitesse de vague avant que le déferlement intervienne. Il suffit pour cela d'initialiser le calcul de la rampe d'accélération, non plus avec une pente de départ de 0°, mais avec des valeurs plus élevées, jusqu’à obtenir la pente de départ qui produit un rattrapage de la vague a 60° (moment du peak). Nous aurons ainsi décrit la condition de "no padlle take off" , ou late take off, correspondant a la stratégie de la force maximale et du temps d'impulsion minimal:

(Rampe d'accélération commençant à 55° logiciel ShaperWaveDynamics)

Nous voyons dans le graphique ci dessus une rampe d'accélération générant un accroissement de vitesse partant de 0 m/s à 52 degré de pente, et atteignant la vitesse de 3.1 m/s a 60°. Remarquons que les forces propulsives (courbe bleu) commencent à 320N à 52° pour monter à 700N environ a 60° au moment du take off. C'est bien une stratégie de la force, même si le surfer ne donne aucun coup de rame!!!

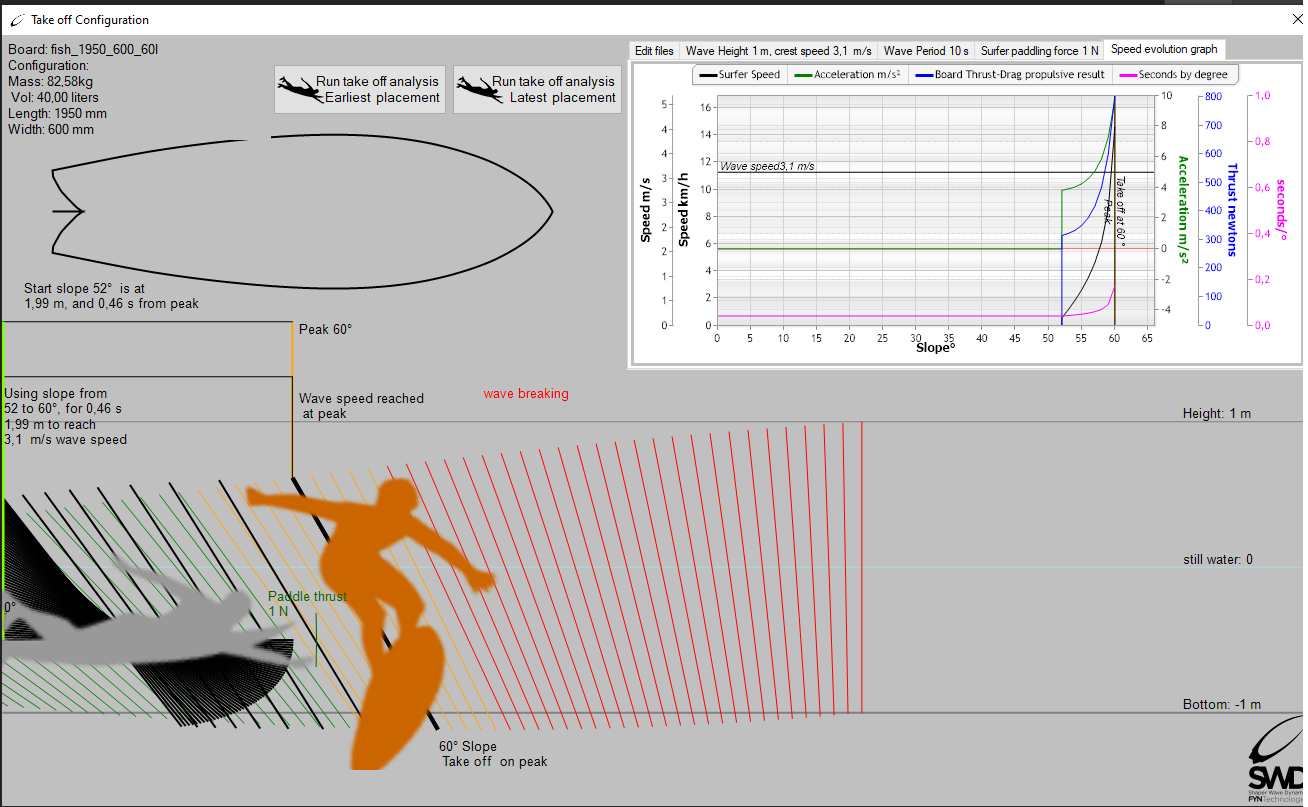
no padlle take off analyse

(Recherche de pente maximale de départ take off: logiciel ShaperWaveDynamics)

Conclusion:

Une planche de volume et forme donnés, produit une traînée hydrodynamique, qui varie en fonction de la vitesse et du poids du surfer. Il est possible de déduire de la courbe de traînée, en fonction de la vitesse, les capacités d'accélération de cette planche et de déterminer, pour une vague de période et de taille donnée, la pente minimale de take off, et la pente de départ maximale pour le surfer et sa planche, dans cette vague.

L’hypothèse de calcul utilisée ici, ne cherche pas a définir précisément des valeurs qui dans la réalité dépendent de plus de facteurs que ceux choisis. Notre hypothèse admet par exemple, un angle de déclenchement du déferlement à 60 degrés, mais cet angle varie en fonction des conditions, par exemple de vent: un offshore, va retenir le déferlement et le repousser de quelques degrés. Mais prendre une hypothèse donnée, et l'utiliser pour comparer diverses planches, est pour l'analyse comparative, la méthode la plus efficace, car elle offre un angle de vue stable et objectif, auquel le shaper et le surfer pourrons se référer pour relier leur expérience à une base théorique stable.

Nous voyons et comprenons par cette approche théorique, que la stratégie de la force n'est pas réservée au surfers puissants, c'est même tout le contraire. Ceci est contre intuitif pour le non initié à la notion d'impulsion, mais devient intuitif et plus clair pour l'initié, qui pourra intégrer la théorie à sa stratégie de placement sur son spot, en fonction de sa planche, l'étude de l'hydrodynamique affûte donc bien notre instinct!

Nous voyons l’intérêt d'un outil de calcul des performances, même si elles restent théoriques, d'une planche donnée, qui donne au shaper et au surfer, une prédiction des aptitudes de la planche au take Off. Mais les qualités d'une planche, en terme de dynamique, ne résident pas uniquement dans les aptitudes au take off, il faudra aussi évaluer les aptitudes de la planche en terme de stabilité et de maniabilité , nous verrons ceci au chapitre manœuvrabilité du surf